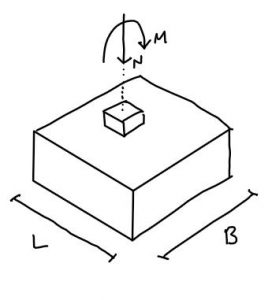
Tensión en una zapata. Comparación de métodos de cálculo
Cómo se puede calcular la tensión que deposita en el terreno una zapata rígida La comprobación de la tensión bajo una zapata suele hacerse suponiendo
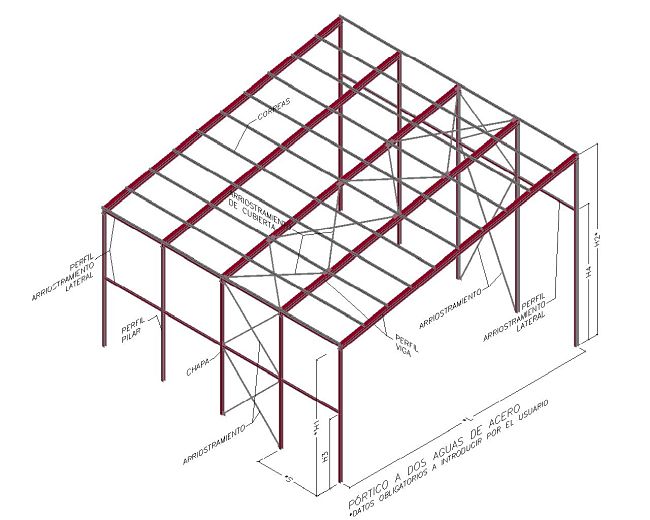
En algunos casos se debe construir una nave adosada a una construcción existente y se emplea como apoyo de la nueva construcción el muro o soportes medianeros de la construcción antigua. Para resolver las consultas sobre este caso de los usuarios de e-STRUC, en este artículo explicamos cómo calcular un pórtico con un solo pilar.
Para poder dimensionar los pórticos de la nueva nave, e-STRUC tiene el procedimiento de pórticos a un agua pero con dos pilares.
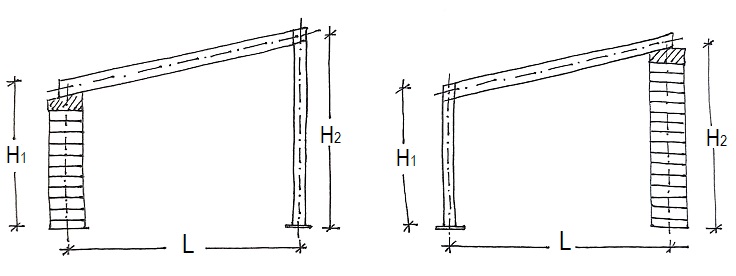
Sin embargo, con este procedimiento se puede también simular el efecto de que exista un solo pilar y que el otro sea el apoyo que proporciona la medianera contigua.
A efectos del cálculo, la diferencia entre uno o dos pilares en el pórtico es la siguiente:
Por tanto, en el análisis del caso sin pilar deberemos simular la ausencia de éste alterando la estructura de un sistema de dos pilares, de modo que los dimensionados sean los mismos en ambos casos. Para ello se imponen las siguientes condiciones para calcular un pórtico con un solo pilar:
Si igualamos ambos casos para las condiciones anteriores, sin alterar la dimensión ni la inclinación de la viga, se obtiene que los pilares han de simularse con un 20% más de longitud del pilar más alto. De este modo se consigue, de manera muy aproximada, que el pilar que sí existe y la viga tengan dimensionados iguales al pórtico simulado.

Al final del artículo podemos ver el cálculo completo hecho a mano. Como se puede ver en ellos, es indiferente a efectos del cálculo que no exista el más alto o el más bajo de los pilares, es decir, que el muro o el apoyo existente estén en la parte alta o en la parte baja del pórtico.
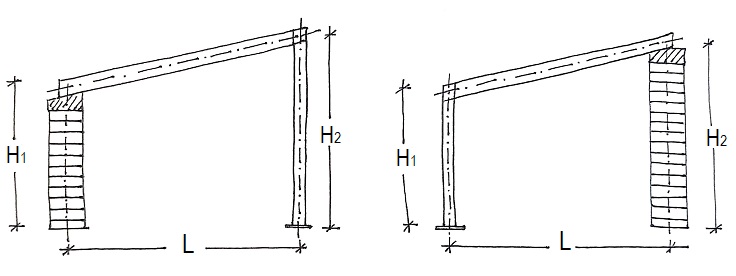
Suponemos, en primer lugar, un pórtico real formado por un pilar de 4 m, una viga de 12 m de luz y un apoyo sobre un muro a 6 m de altura, como en el esquema:
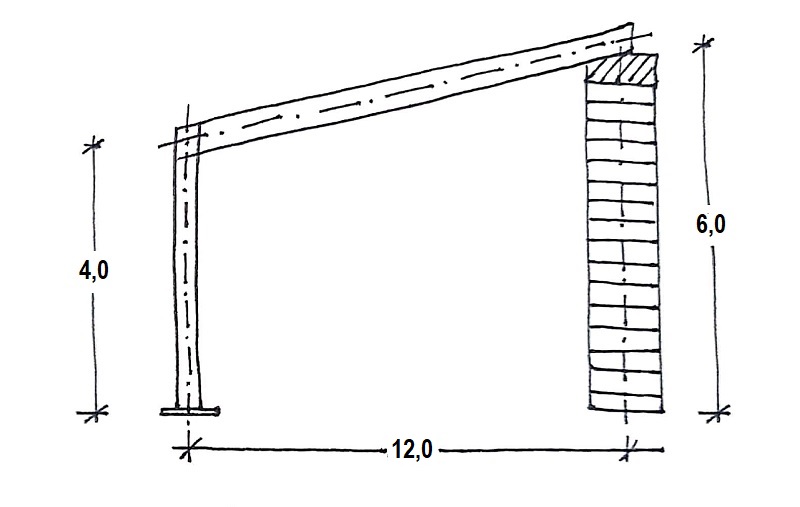
La nave mide 27 m de longitud y los pórticos están cada 3 m.
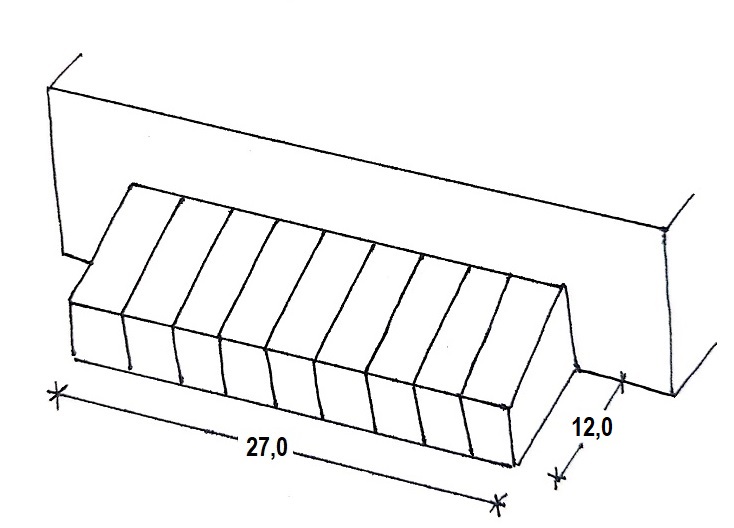
Los datos, si se tratase de un pórtico con dos pilares y una viga, serían:
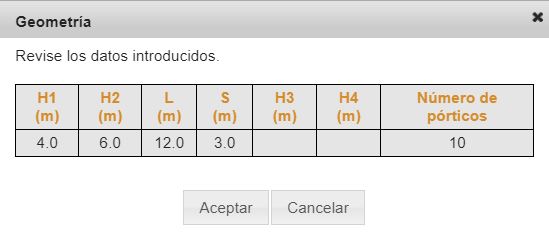
Continuamos con la introducción de los datos de secciones y materiales, los cuales marcamos como desconocidos para que e-STRUC escoja los tipos más apropiados. Si los tipos y calibres no nos encajan en el proyecto podemos modificarlos al final del cálculo.
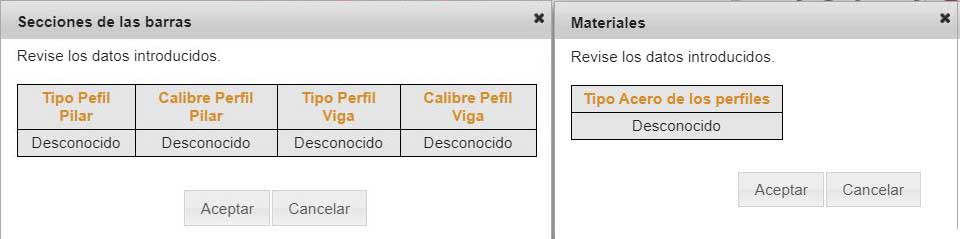
Los datos constructivos son:
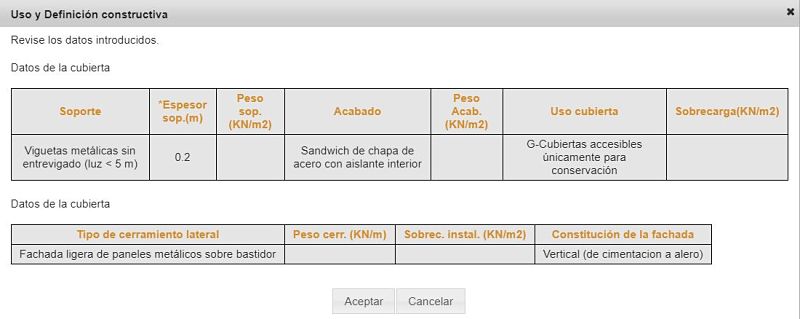
Introducimos los datos de entorno y clasificación de sismo:
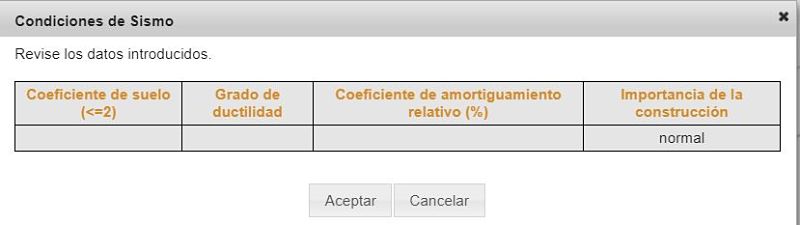
Y, finalmente y los correspondientes a la ubicación de la construcción, que puede ser marcando la ubicación en España:
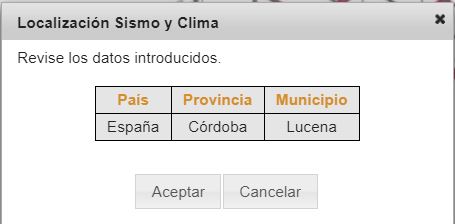
O indicando la sobrecarga de nieve, presión dinámica de viento y aceleración básica y coeficiente K de sismo, si el lugar de nuestra edificación no está en España:
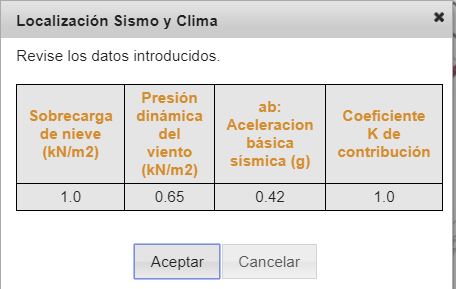
El resultado es un pórtico formado por dos pilares HEB 220 y una viga HEB 260

Para hacer la simulación y calcular el pórtico con un solo pilar con e-STRUC, basta con modificar las dimensiones de los pilares.
Como hemos visto, se hace todo igual pero se le añade un 20% de la altura del pilar más alto a ambos pilares. En este caso el pilar más alto es el muro, por lo que debemos añadir un 20% a los 6 m. Añadimos, 1,20 m de altura a ambos pilares. Los pilares medirán por lo tanto, 5,20 y 7,20 m respectivamente, con lo que la geometría sería:
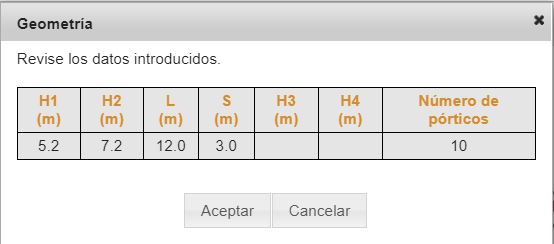
Todos los demás datos son idénticos al pórtico calculado en primer lugar, con lo que no es necesario repetirlos aquí.
El resultado obtenido es un pórtico formado por pilares y viga HEB 260. Por lo tanto la estructura estará formada por un solo pilar y una viga, ambos HEB 260.
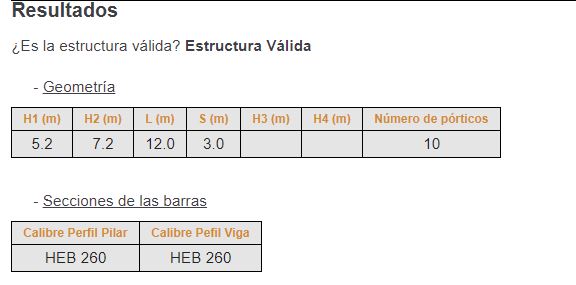
En los planos descargados debemos sustituir únicamente el apoyo del muro, manteniendo el apoyo del pilar, y el nudo pilar-viga. En necesario ajustar las dimensiones de los pilares, ya que están aumentadas un 20%. Los arriostramientos de la estructura obtenidos para la cubierta y el lateral de pilares nuevos son válidos. En el apoyo existente, si es un muro resistente no será necesario colocar arriostramientos, y si se trata de pilares deberán estar arriostrados.
Debe tenerse en cuenta que los resultados de la memoria de e-STRUC serán los correspondientes al pórtico simulado. Los valores de las solicitaciones máximas, y las de las deformaciones de control sí son los mismos, pero no las gráficas, por la razón de que la geometría no es la misma.
Así resolvemos el cálculo, con las dimensiones de la viga y el pilar, los apoyos y uniones. Obtenemos los valores de las solicitaciones, asegurando que la construcción es válida y cumplirá con todos los requisitos de la normativa vigente.
El desarrollo del cálculo es el siguiente, considerando que las variables que no son prima, son las de la geometría real, y los valores con prima, son los del modelo simulado:

Si te ha gustado nuestro artículo te agradecemos que lo compartas en tus redes sociales, a través de los enlaces que tienes abajo. ¡Y esperamos tus comentarios!

Cómo se puede calcular la tensión que deposita en el terreno una zapata rígida La comprobación de la tensión bajo una zapata suele hacerse suponiendo
Desarrollada con dedicación exclusiva por Euteca, la consultora de estructuras líder del mercado hispano
Calcular rehabilitación de cimentaciones
Calcular rehabilitación de muros
Calcular rehabilitación de forjados
Calcular zapatas
Calcular muros de contención de sótano
Calcular estructuras de acero
Calcular estructuras de hormigón
Calcular estructuras de madera
Calcular pilares
Calcular pórticos