Hay otros casos, como puede ser el viento o el sismo, que siendo acciones netamente variables con el tiempo, podemos emplear casi siempre modelos estáticos equivalentes.
En este artículo vamos a analizar las principales ideas sobre el comportamiento dinámico de las estructuras, es decir, en relación a la variación de cargas sobre ellas respecto al tiempo, cuando esta variación es muy relevante para la estructura.
Cuando las acciones tienen una variación relevante con respecto al tiempo, entonces el comportamiento de una estructura no es estático, sino que se considera dinámico, es decir, que la respuesta de la estructura varía con el tiempo, lo mismo que las acciones. Pero, eso sí, no tiene por qué suceder que las acciones y la respuesta de la estructura varíen simultáneamente.
Por comenzar con las ideas básicas sobre el comportamiento dinámico de las estructuras, vamos a ver cómo sucede el equilibrio de un cuerpo si se lo aparta de su posición de equilibrio estático. Supongamos lo más sencillo: un mástil con poca masa -despreciable-, con una masa relevante en su punta, empotrado en el suelo. Sería el modelo de una torre de control, de una torre de vigía, de un palomar de campo,… Supongamos que no hay viento ni ninguna otra acción externa. En tal caso, si apartamos la masa de la vertical del mástil, en dirección horizontal, y la soltamos, sucederá que la rigidez horizontal del mástil generará una fuerza proporcional al desplazamiento inducido que tenderá a devolver la estructura a su posición inicial.
Pero al moverse la masa, aparece sobre ella la fuerza dinámica debida al producto de su masa por la aceleración que adquiera. Ésta, la aceleración, deriva del movimiento -es la segunda derivada del desplazamiento con respecto al tiempo- y, por tanto, estará ligada a cómo se mueva la masa. El equilibrio obliga a que la fuerza procurada por la rigidez del mástil y la derivada de la aceleración de la masa se anulen, es decir, la suma de ambas fuerzas debe ser nula. Pues de esta condición se derivan dos consecuencias fundamentales.
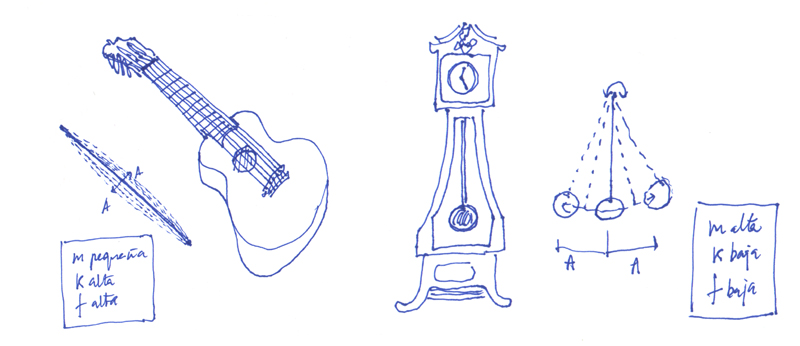
La primera es que el movimiento de la masa en torno a la posición de equilibrio estático es una ley sinusoidal función del tiempo. Es decir, es un movimiento vibratorio con una frecuencia determinada -llamada frecuencia fundamental-. Y la segunda es que dicha frecuencia f es un valor constante que depende de la relación entre la masa m y la rigidez del mástil k, según la expresión:
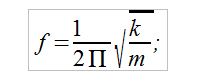
Esta frecuencia mide el número de vibraciones completas por unidad de tiempo, y su medida es el hercio (Hz). Su inversa, el tiempo que tarda en realizar un ciclo vibratorio completo, se denomina periodo, nombrado con T, y se mide generalmente en segundos (s).
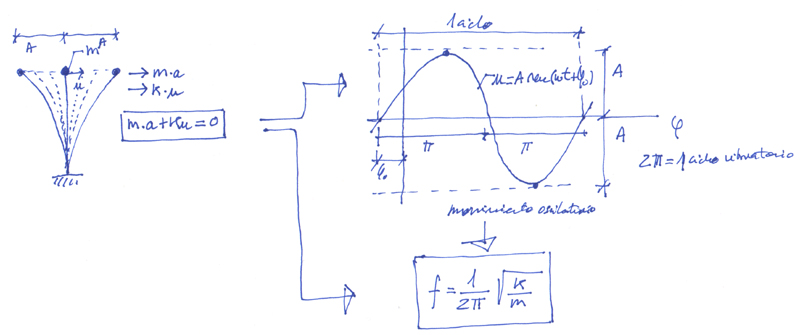
Así pues, sucederá que un cuerpo con gran rigidez y poca masa tenderá a oscilar con una frecuencia alta -una cuerda de guitarra, por ejemplo-, mientras que algo de poca rigidez con masa grande, presentará frecuencias bajas (oscilará lentamente) -un péndulo de reloj, por ejemplo-. Hay otra cuestión importante y es que en el movimiento vibratorio aparece la variable de la amplitud del movimiento, A, -cuánto se separa la masa de su posición de equilibrio estático- y resulta que la frecuencia es indiferente respecto de la amplitud.
Por tanto, no importa cuánto separemos inicialmente la masa de su posición estática original, porque la frecuencia del movimiento vibratorio será la misma para cualquier amplitud del desplazamiento.
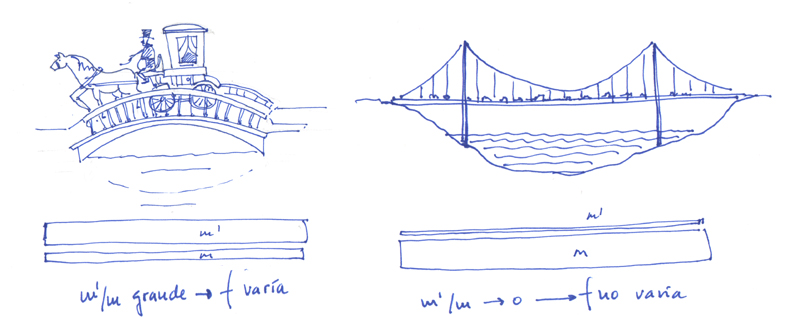
Los ejemplos antes indicados no contienen gran complejidad en principio, porque la masa del cuerpo es constante: la masa de la cuerda o la del péndulo. Pero en una construcción resulta que tenemos las masas debidas al peso propio y las de los añadidos permanentes a la construcción (acabados, tabiques, solados, etc…), que no varían, están siempre. Sin embargo, aparecen las sobrecargas, que son masas cuyas magnitud y posición pueden variar. Entonces, en tal caso, para cada disposición de masas sobre el cuerpo aparecerá una frecuencia distinta de comportamiento vibratorio del sistema.
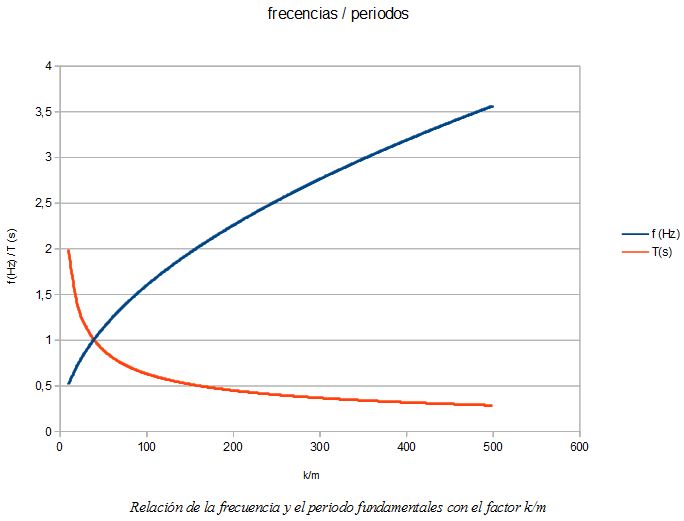
Otra de las ideas básicas sobre el comportamiento dinámico de las estructuras es que la rigidez de la estructura, k, es un valor constante y es propiedad de la estructura, lo mismo que la masa m debida al peso propio y las cargas permanentes, por lo que si no hay sobrecargas la frecuencia fundamental, f, no variará. Pero si hay sobrecargas de masa m’, la frecuencia se alterará en función de cuánto valga esta última. Por tanto, la frecuencia fundamental f es una propiedad de la estructura para una determinada distribución y magnitud de las masas m y m’, de las cargas permanentes y las sobrecargas, respectivamente.
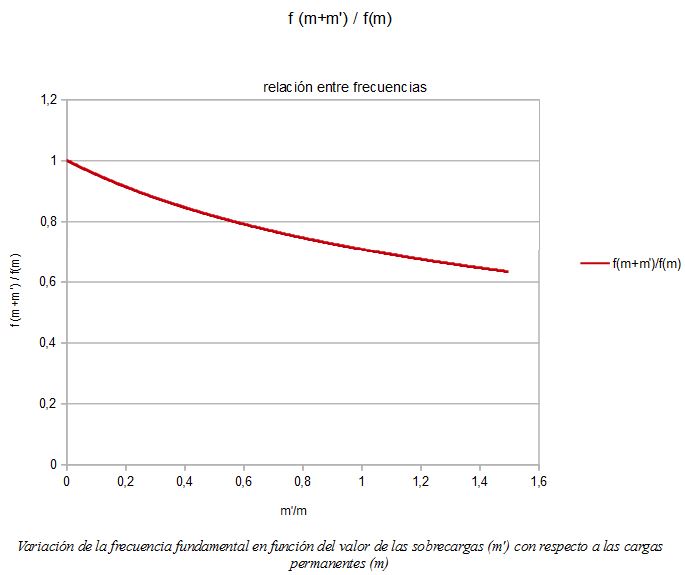
Así, en construcciones de gran tamaño -un puente, un edificio de estructura potente-, casi toda la masa es debida a las cargas permanentes y sólo una parte ínfima es debida a las sobrecargas, con lo que la variación de la frecuencia f es prácticamente nula. En el caso opuesto, una estructura ligera con masas debidas a sobrecargas relevantes -una pequeña pasarela peatonal, por ejemplo- la frecuencia f variará enormemente en función de la sobrecarga.
Esto, veremos, es fundamental, y por lo tanto es otra de las ideas básicas sobre el comportamiento dinámico de las estructuras.
Cómo se puede calcular la tensión que deposita en el terreno una zapata rígida La comprobación de la tensión bajo una zapata suele hacerse suponiendo
Desarrollada con dedicación exclusiva por Euteca, la consultora de estructuras líder del mercado hispano
Calcular rehabilitación de cimentaciones
Calcular rehabilitación de muros
Calcular rehabilitación de forjados
Calcular zapatas
Calcular muros de contención de sótano
Calcular estructuras de acero
Calcular estructuras de hormigón
Calcular estructuras de madera
Calcular pilares
Calcular pórticos
2 comentarios en “Ideas básicas sobre el comportamiento dinámico de las estructuras I”
Que buen artículo!
Es notable la forma y el buen manejo que se le da a tan fabuloso tema como son nuestras amadas Estructuras y sus formas de moldearlas y cambias paulatinos por el tiempo y las circunstancias!
Compartiré este post con mis conocidos!
Muchas gracias, Andrés, por tus felicitaciones y por compartirlo. Saludos