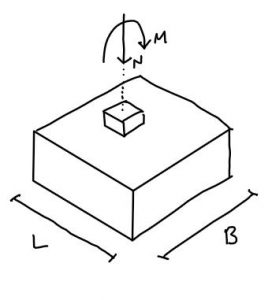
Tensión en una zapata. Comparación de métodos de cálculo
Cómo se puede calcular la tensión que deposita en el terreno una zapata rígida La comprobación de la tensión bajo una zapata suele hacerse suponiendo

Como definición, podemos decir que se llama esfuerzo cortante en una barra a la fuerza que es paralela a una sección recta de la misma.
Siguiendo con las solicitaciones o esfuerzos en las estructuras de barras, nos ocuparemos ahora del cortante.
Se denomina cortante porque esa fuerza paralela a la sección tiende a “cortar” la barra por dicha sección, como vemos en la imagen de portada con la barra de pan. En el caso del esfuerzo cortante en estructuras sí que es totalmente indiferente el signo de la fuerza, sin que cambie en nada el efecto mecánico en la barra, siempre y cuando su sección sea simétrica. Si la sección es asimétrica, el signo del cortante sí altera el comportamiento mecánico de la barra.
Tomamos de nuevo como ejemplo de estructura sencilla la formada por la percha del pozo, la cuerda y el cubo con agua que vimos en el artículo sobre el esfuerzo normal. La carga es el cubo con el agua, las reacciones aparecen en ambos apoyos de la percha. El cortante es el esfuerzo interno que se produce en los bordes de la zona rayada de la percha.
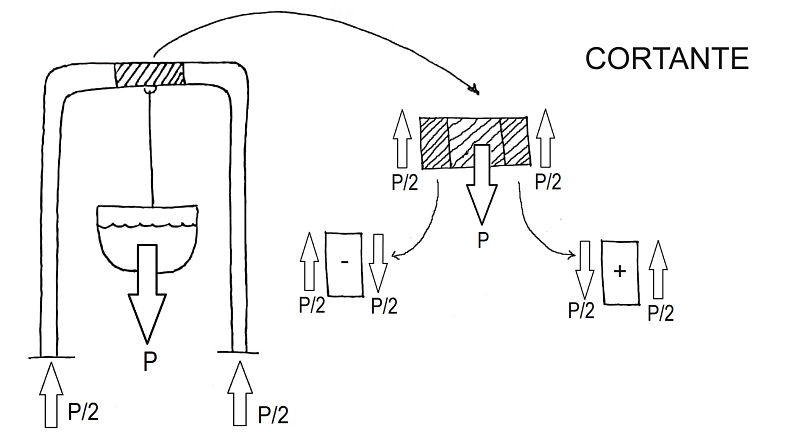
Del mismo modo que la fuerza normal, el cortante se resiste gracias a tensiones en el material de la barra, y que son paralelas y de igual signo que la fuerza. Por tanto, en este caso se trata de tensiones paralelas a la sección, que se denominan tensiones tangenciales. Por mero equilibrio, estas tensiones son idénticas en un punto en dos direcciones perpendiculares. Es decir que en un punto determinado de una sección, la tensión tangencial en la sección de la barra es la misma que en un corte longitudinal de aquélla.
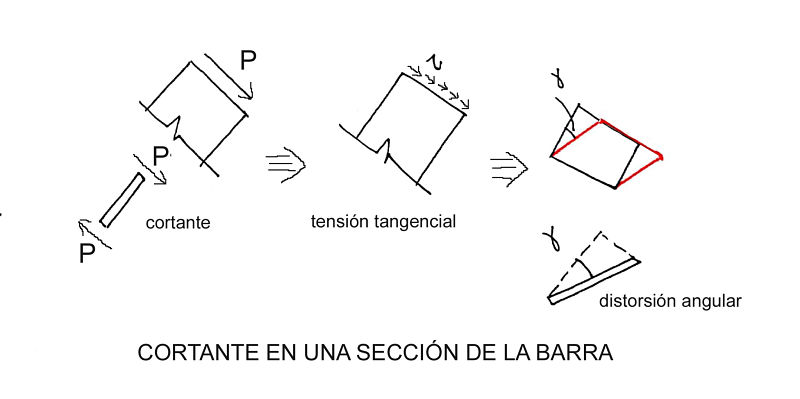
En el caso de las tensiones tangenciales la deformación asociada no es un incremento o decremento de longitud unitarios, sino una distorsión angular unitaria.
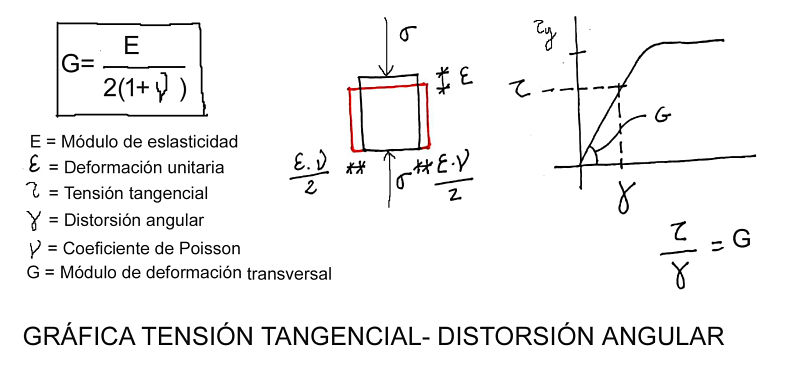
Igual que el caso de las tensiones normales, las propiedades del material rigen la deformación de una barra sometida a cortante. En este caso, la propiedad de referencia es el módulo de deformación transversal, G, que depende del de deformación longitudinal, E, y del coeficiente de Poisson. Este coeficiente mide cuánto se deforma un material en la dirección transversal a una deformación longitudinal. El valor de G mide la tensión tangencial para la cual un paralelepípedo sometido a ella adquiere una distorsión angular de un radián.
También la resistencia de la sección ante un esfuerzo cortante en estructuras está ligada al límite elástico del material, si bien para un valor menor que éste. Hay que incidir en que, así como en los esfuerzos normales las tensiones se distribuyen uniformemente en la sección de la barra, no ocurre lo mismo con las tensiones tangenciales, que son forzosamente nulas en las fibras extremas de la sección y alcanzan su máximo en el interior de la sección.

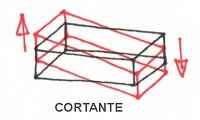
Entonces, cuando una barra está sometida a esfuerzo cortante, la barra tenderá a distorsionarse saliéndose de su directriz, pero sin que las secciones de la barra giren en absoluto, como en el esquema dibujado más abajo. Aunque es poco común que una barra presente sólo esfuerzo cortante. Que la distorsión sea en un sentido u otro, perpendicular a la directriz depende del signo del esfuerzo cortante, pero no hay diferencia cualitativa por el signo.
Si te ha interesado el artículo te agradecemos que lo compartas en tus redes sociales, más abajo tienes los enlaces. También te invitamos a que nos dejes algún comentario, que responderemos encantados.

Cómo se puede calcular la tensión que deposita en el terreno una zapata rígida La comprobación de la tensión bajo una zapata suele hacerse suponiendo
Desarrollada con dedicación exclusiva por Euteca, la consultora de estructuras líder del mercado hispano
Calcular rehabilitación de cimentaciones
Calcular rehabilitación de muros
Calcular rehabilitación de forjados
Calcular zapatas
Calcular muros de contención de sótano
Calcular estructuras de acero
Calcular estructuras de hormigón
Calcular estructuras de madera
Calcular pilares
Calcular pórticos
4 comentarios en “El esfuerzo cortante en estructuras”
Gracias por aclarar mis dudas. Que bueno poder contar con artículos como este y por este medio para seguir superando nos de forma fácil.
Muchas gracias a ti por tus comentarios.
Es una gran herramienta el apoyo que estos artículos brindan y una herramienta preferente para lograr algo más útil. Es mejor que mucha otra información comercial o de poca utilidad. Espero poder seguir encontrándola.
Gracias Rodolfo!
Seguiremos incluyendo información.
Un saludo.